Stream Cipher design postulates / SQ model

Kostadin Bajalcaliev
Institute of Informatics -Skopje
kbajalc@eon.pmf.ukim.edu.mk
http://eon.pmf.ukim.edu.mk/~kbajalc

Abstract

1. Introduction

"Stream Cipher" is algorithm which produce Secure Pseudo Random Sequence of bits. Opposite to Block Ciphers where the plaintext is run trough a sequence of key-determinate transformations, stream ciphers produce a bit-sequence independent of the plaintext. Figure 1 illustrates the general concept of Stream Cipher.

Any stream cipher has these components. Using the standard mathematical notation the stream cipher can be described as:

W is a finite set of states, F is the State Update Function, OGF is a function generating the cipher output bit(s) according to the current state. Definition of W is of crucial importance, because the Stream Cipher is determined by the set of internal states. One of the simplest PRNG is the Congruent Generator.

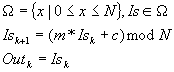
The presence of all crucial elements is obvious. The OGF is an identity function, F is a simple linear transformation with a single parameter m; m and the initial state is the "key".

The objective of this thesis is to define the basic criteria for stream cipher design. The major questions that this thesis is concerning can be summarized as:

1. 1.  
   2. Defining the role of each SC component?
   3.  
   4. What are the basic criteria in order to design statistically good SC?
   5.  
   6. What are the basic requirements for designing secure SC?
   7.  
   8. Is there a method of designing provably secure SC?

2. Basic definitions and assumptions

Since the discussion here is mostly concern with randomness; a precise definition of the term is obligatory.

Any process which prediction requires more information than available in the system, can be assumed unpredictable. Theoretically everything is predictable but it is not so in practice. Predictability as a concept can only be applied to processes, running in finite set of possible states. Or, anything than can be represented digitally without lost of information is predictable e principum. By definition anything produced by deterministic algorithm is predictable, assuming that all the information produced by the process is enclosed in the system. Crucial definition needed:

The last definition is of little practical value, so restated and applied to discrete system it is:

ECF in practice is the maximum rate of compression possible. A fundamental concept we need to understand the stream ciphers and continue the discussion is Entropy-Neutral Transformation .

Any injection function is Entropy Neutral. For example the S-box [1,5,3,0,4,2,7,6] is EN, if the sequence transformed according to this S-box have ECF = k, than the transformed sequence will have the same ECF. But S-box [1,5,2,1,4,5,3,7] will cause a lost of entropy, because it is not an injection. No transformation that will increase the entropy exist. Since we are more interested in dynamical transformations [where the transformation rule change over the time, and mathematical concept of injection and bijection is generally inapplicable] the concept of Quasi Entropy Neutral Transformations is introduced.

Because the concept of randomness is inapplicable in discrete systems, Pseudo-Randomness is introduced.

Whenever in this thesis is stated that a given sequence or process is random, than means than the sequence pass the polynomial statistical tests of randomness.

Assuming the existence of random sequences, the following statements are applicable.

1.  
2. If A is a random sequence then any subsequence of A is random too.
3.  
4. If A is a random sequence and B is or it is not a random sequence than C=A*B (where * is any EN operation such as +,xor,-) is also a random sequence
5.  
6. If A is a random sequence and A’ is a sequence formed from randomly (but not obligatory sequential) chosen elements of A, than A’ is a random sequence.
7.  
8. Discarding parts of a random sequence A by a fixed rule results in random sequence A’.
9.  
10. If C is a complex transformation C=AB, y=C(x)=A(B(x)); then ECF(C) £ min(ECF(A),ECF(B))

The 5^th assumption explains why the S-boxes should be permutation (EN transformation), in opposite case the algorithm using non EN s-boxes is potentially weak. In order to test some complex transformation to confirm EN status it is enough to show that the 2^nd assumption is satisfied for each component transformation.

3. General SC model

The stream cipher is an iterative function, the n-th output is defined in terms of the previous outputs and the current state. Here is simple construction:

The Internal State is defined as a state of the permutation P. The Internal State Update Function is the second step [Swap(Counter,Out_k-1)], and the Output Generation Function is the third. The initial value of P and the counter can be used as a KEY.

The Counter is needed to insure over-time character of the function. If it is excluded than it is very possible the generator to enter a cycle [period] - significantly shorter then the expected one. Theoretically the cipher above should have a period of length N!*N, in practice the maximum period is unattainable.

The Internal State Update Function. Since the stream ciphers should be Dynamical Objects, there must be some time-depend function which update the internal state.

The Output Generation Function realize the objective of the Stream Cipher to produce some output values according to the internal state and the previous outputs.

Starting form the mathematical model of Stream Ciphers as iterative function and incorporating the basic SC concept presented. The SQ model is build in the following way:

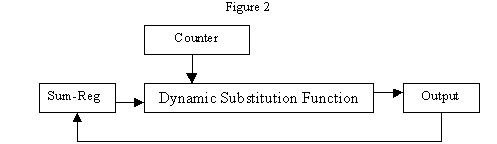
Any discrete function can be tabulated. The set of possible function over GF(N) is N^N the cardinality of the set of possible variation over the set {0..N}. Because of reasons discussed letter only the injection functions are of interest in Stream Cipher design. Injection function defined over a finite set, by definition is permutation of the whole set or a part of it. The set of possible Substitution Functions over finite set have cardinality N!. The Figure 2 shows the main idea behind SQ.

The idea is to build the cipher using dynamic function (P). This idea is originally introduced with RC4, and T. Ritter does further development. The next chapter presents the evolution of this idea into a real PRBG, using simple example constructions.

4. Simple Constructions

EC-0 is the simplest generator embodying the model presented before. Nothing serious can be expected from this extremely simple generator.

Making only one small change by adding the Sum Registry into the design, the properties of the generator are significantly improved.

Unexpected for such a simple construction EC-1 passes DIEHARD tests. Why it is so? In order to answer that question it is important to see what will happened if some of the needed components are excluded.

This construction does not pass DIEHARD. Excluding the counter makes the generator extremely weak, the entering in a short cycle is expected. Here is a slight improvement:

This is also a weak construction. What ever to be changed the generator without a counter will always fail to produce pseudo random numbers. The Counter structure is obligatory.

EC-4 is generator without a Sum Register:

It is obvious that there are structures that improve the randomness of the generated sequence, and those sabotaging it. Adding the non-linear-sum-register has shown to be a good change. Changing the output generation function into Out_k=P[P[Counter]+P[Out_k-1] mod N] also. The following generator implements all those improvements.

This is a strong pseudo-random generator showing that SQ model introduces a sufficient number of criteria to build a PRNG.

5. Security Analysis

The problem of Stream Cipher security is closely tied with several mathematical concepts: non-linearity, one-way functions and unpredictability. The existence of one-way functions is still under debate, however for this thesis needs it is enough to define a one-way function as irreversible. It is important to notice that a certain function [transformation] can be injection [entropy neutral] and in the same time the reverse function to be unexacting. Simple examples are the EC ciphers presented above.

For simplicity of the analysis, it can be assumed that Counter and Sr are absolutely independent [every pair (Counter, Sr) is equally probable]. This transformation is N^2® N mapping, in order to have a good statistical behavior and it is important to be uniformly distributed over N, which is the case. For example the following transformation will not produce a uniform distribution.

As stated before, each function like f(x)=g(x)+x or f(x)=g(x)+f(g(x)) will not show a uniform distribution.

If this kind of function is used, the cipher will be biased as a result of losing entropy from the system.

This simple program will most probably halt, or at least enter a cycle with maximum length N/4, where N is length of the permutation. This is just a confirmation of the principle introduced in this thesis, stating that each elementary transformation [all the steps] must be Entropy Neutral.

This version of the cipher shows miserable results when tested with DIEHARD. Only simple change in OGF step is solving the problem instantly.

The last question about the statistical properties of SQ-model stream cipher is how the randomness is generated, since the random behavior of some of the previous simple construction is demonstrated.

The COUNTER is a simple function f(x)=x+1 mod N; by definition this is a Entropy Neutral transformation. Trivially GF(N) is closed over the addition. The COUTER is a transformation N® N having a uniform distribution, the Org(f)=Im(f)=N.

SUDF is realized as simple swap, if W is a set of all permeation over the set {0..N} and F is transformation defined as F(P,i,j) = Swap P[i], P[j] where P Î W , i,j Î N; then W is closed in respect to the transformation F. For any possible values of P,i and j the result will be element of W . Even more for each pair P,Q permutation Î W there is at least one sequence of pairs (i,j)₁ (i,j)₂ … (i,j)_w such as F(F(….F(P,(i,j)₁),(i,j)₂)…….),(i,j)_w)=Q. (W ,F) is a group [even F is not a operation in mathematical terms]. SUDF is a transformation W ´ N ´ N ® W , Org(F)=Im(F)= W .

OGF - the simplest form of this step is Out=P[Sr], or the improved modification Out=P[P[Sr]] in order to escape using the control signal in the same way twice. A similar discussion as that about SUDF hold in this case. Any permeation of {0..N} is P: N® N mapping, by definition permutations are injections, the same holds for any k P^k: N® N.

NLS, this is an important step using left-circular-shift inexpressible with nether of the previously defined operations or functions. It is impossible to express left-circular-shift with additions, nor using the P function.

The important characteristic is that neither of the transformations used is expressible trough the others.

Attacking some of EC generators is trivial, the analysis of EC-1 will demonstrate the general concept.

This generator passes DIEHARD with N=256, have a long period, it is unsecure?

1. 1.  
   2. The output sequence is available to the attacker, Out_n, Out_n+1, Out_n+2 ...
   3.  
   4. The value of Sr_n can be found by brute-force since there are only 256 possible values, also the Counter
   5.  
   6. Reversing the generator is easy
   7. Sr_k+1=(Sr_k<<<1)+Out_k
      P[Counter+Sr_k mod N]=Out_k
      Swap P[Counter], P[Sr]
      Counter++
   8. Stop when IsAPermutation(P) is true
   9.  
   10. Continue generating the rest of the stream

This simple anti-generator will recover the internal state because Out sequence carry sufficient information about the internal state, each output reveal the value of one P entry. This is impossible with EC-5 because Out_k=P[P[Counter]+P[Sr] mod N]. Knowing Counter and Sr is enough to recover a value of P entry because P[counter]+P[Sr] is clearly P-depended. EC-8 presented later is even harder to reverse since Sr_k+1=P[(Sr_k <<<1)]+Out mod N, using this OGF cause Sr to be non-computable from the output values.

There is a simple solution EC-1 like cipher security problem. Before defining the idea how to make provably secure SC, here is a little illustration story.

Let G is a 8-bit generator, discarding the first bit result in ZYYYYYYY, where Z is the discarded bit. Let Z’XXXXXXX and Z’’YYYYYYY be two successive values produced by the generator Z’YYYYYYY=F(…,Z’’XXXXXXX); but Z’ and Z’’ are unknown so there 4 different equates and only one of them is the true.

This is possible since the iteration of SQ is Function taking as input the non-linear-sum of all previous values produced. Any attack on SQ-like ciphers will require the knowledge of (control signal, output) pairs in order to reconstruct the internal state.

If the attacker have only the secondary output available, then it is impossible to compute Sr_k. In order to launch an attack considerable long sequence of primary output should be available to the attacker, which should be prevented by a correct implantation.

Since the bit discarding is impractical, regarding the speed of the generator, NLS can be made P-Depended.

Making NLS State-depended enable to use all the bits of the generated output. Knowledge of all previous outputs is not enough to compute Sr_n value, the original state of P and all consecutive states are also needed in order to compute Sr having the output of the generator, but the state of P is exactly what the attacker is truing to discover! Making the NLS P-depended close all the ways that can lead to the knowledge of the internal state.

6. Quasi EN transformations

Using dynamically changed permutation and other static EN transformations is the core of SQ-like ciphers. As the results of testing the Example Ciphers have shown this approach be suitable for Stream Cipher design. The cipher constructed according to those principles is a Quasi EN Transformation. Assume that EC-8 is modified to act as a substitution box.

This is an example of Quasi-EN-Transformation according to the D8. But are only the EN transformations usable as building blocks for SC? Any transformation that produces a uniform distribution can be utilized as QENT. It has been shown that EN transformations can be used to build QENT, but can non-EN transformation be used also? I have no answer to this question, however the following construction has passed DIEHARD tests.

The core of this generator is a variation-V, which by definition is not Entropy Neutral. But the whole construction has shown to be QENT. It is very interesting to examine a mixed construction using both Permutation and Variation as Core element. SQ1-R is realization of this idea. It is very interesting that hybrid construction using both EN and non-EN can be QENT and can show excellent statistical properties. This is because of the first assumption introduced in the beginning of this thesis. Using EC-8 and EC-9 as a starting basis a combine generator is be constructed.

It is enough at least one part of the generator to show the expected statistical randomness. Since it can be experimentally confirmed that both EC-8 and EC-9 pass statistical test of randomness it can be assumed that the combined generator will also, which is the case.

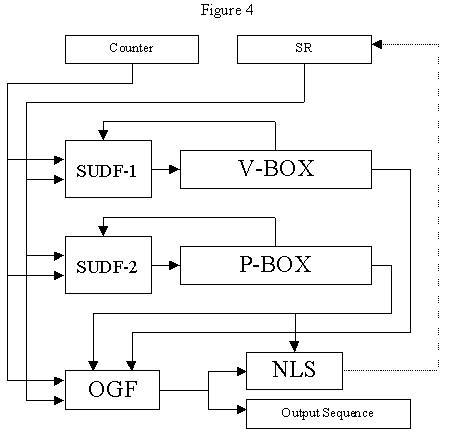
Figure 4 presents the structural diagram of EC-10. SUDF-1 is updating the state of V, SUDF-2 is updating the state of P, OGF according to those updates calculate the output value, according to the produced value and previous state the value stored in Sr is updated. This construction is just a simple combine generator of EC-8 and EC-9 - both existing in their integral form. Only the OGF function is changed to combine the values produced by both the generators.

7. Conclusion

This thesis objective was to provide answer to a general question: "Defining general model for stream cipher design" Summarizing what have been presented before it can be concluded that this thesis has provided an answer. SQ model and the design criteria described here have shown to be sufficient to design a stream cipher.

Definition of the role of each SC component

What are the basic rules in order to design statistically good SC?

1. 1.  
   2. The SC must be QENC transformation, each step must be ENT.
   3.  
   4. All values used by the algorithm must be affected by self-mutation, non of them should enter the next iteration unaffected
   5.  
   6. All transformations used should be based on as independent as possible parameters

What are the basic requirements a given SC to be secure?

Is there a method of designing provably secure SC-s?

Appendix 1

The SQ1-R Stream Cipher

1.  
2. Data Structures
3. SQ1 is word-oriented algorithm; any word size is supported respecting the available memory. In order to implement SQ1 data structures below are required: (given in C notation)

   P[w] – permutation of numbers from 0 to w
   V[w] – variation, every element can have any value 0 to w
   Sr - feedback register

   * All data types are (log₂ W)-bit long, all the arithmetic is done modulo W

   The word size can be some conventional value 8,16 … bits, but the formal definition of the algorithm assume any value with respect to available memory. In the real implementation other variables are used but they are meter of optimization.

4. Notation and SQ Primitive Operations

1.  
2. Addition of two words, denoted by "+", addition is done modulo 2^w
3.  
4. Bit-wise exclusive OR of words, denoted by XOR
5.  
6. A circular-shift rotation of words: the rotation of word x left by y bits is denoted x<<<y
7.  
8. Modulo, x modulo y equal z denoted x mod y = z.

A left-rotation of fields: X’[y]=X[y+z mod field_size], denoted by X<<<z is basic operation in SQ1, it is not primitive but easily deliverable from the primitive operations.

1.  
2. Algorithm Specification
3. According to definition of data structure and primitive operations here is algorithm formal definition:

   /* Initialization */
   for j=0 to 2^w { P[j]=j; V[j]=0; }

   /* Generator iteration */
   {1} QC=P[V[Sr]];
   {2.1} V[Sr]=V[Sr]+QC;
   {2.2} V[QC]=V[QC]+Sr;
   {3.1} Swap P[Sr], P[QC];
   {3.2} P<<<1;
   {4.1} Index=P[Sr]+P[QC];
   {4.2} Out=P[Index]+V[Index];
   {5} Sr=P[Sr<<<1]+Out;
   Return Out

   SQ1-R is very simple, that can be encoded as a function, which produce values according to its internal state. The state of the generator is defined with P[], V[] and Sr.

4. Keying SQ1
5. In SQ1-R as most of Stream Ciphers "keying the generator" is setting the initial state. Very simple strategy is used. The key stream is feed into Variation V[] and the key length is feed into Sr. First 2^2w outputs are discarded to "worm up" the generator. Here is the formal definition of keying procedure.

   K[0..L] is the key
   L is length of the key
   r=0;
   For j=0 to 2^w { V[j]=K[r]; r=(r+1) mod L; }
   For j=0 to 2^2w SQ1();

   SQ1() is the generator function described before. The key should be the same word size as P[] and V[] but it is allowed to be smaller to. For example if w=14, the key can be conventional 8-bit character field. If the w<8 (what is very bed idea) that the key should be cut in w-bit peace in order to feed it into V. The maximal key length allowed using this strategy is 2^2w bits, the length of V in bits.

6. Implementation Remarks

Because of security of the algorithm please follow these remarks:

1.  
2. SQ1 is not intending to be secure for any word size or key length. The word size should be greater than 8bits.
3.  
4. It is recommended not use all the bits produced by the generator, discard at least one. Since the processing time in software implementation will be the same this security enhancement can be used. If 8-bit values are needed to encrypt files or communication channels use 9-bit word. The values produced by the generator are going to be 0..511, just discard the MSB.
5.  
6. Be careful chousing key.

SQ1 is a fast algorithm, generating 1MB take 1.2 sec using my Celeron 300 (RC4 require 1 sec). However SQ1 offer you more security than any other Stream Cipher.

1.  
2. Design Rationale
3. SQ-R is a improvement of ExampleCipher-10 described in "Stream Cipher design postulates – SQ model". EC-10 show excellent statistical properties, P-based algorithm and V-based algorithm in EC-10 are further integrated to produce a monolith structure.

   EC-10
   Permutation P[0..N]
   Variation: V[0..N]
   Counter
   OutV – Output produced by the V-based sub-algorithm
   OutP – Output produced by the P-based sub-algorithm
   Out - Sum Output
   Sr - NonLinearSum
   

   Counter++
   V[Counter]=V[Counter]+Sr
   V[Sr]=V[Sr]+Counter
   OutV = V[Counter] + V[Sr]
   A=P[Sr]; B=P[Counter]
   Swap P[A], P[B]
   OutP=P[P[Sr]+P[Counter]]
   Out=OutV+OutP
   Sr=P[Sr<<<1]+Out

   The main idea is to substitute the counter with a quasi-counter structure, instead of having a independent V-base sub-generator, V is used as a pool of randomness which in an unpredictable way collect randomness produced but the previous iterations.

   {1} QC=P[V[A]];

   This is the quasi-counter step. The values produced are unpredictable because all previous states as well as the initial configuration are needed to reconstruct the value of QC in any moment of time. The counter was the only independent step in EC-10, and by definition its value is available to the attacker.

   {2.1} V[Sr]=V[Sr]+QC;
   {2.2} V[QC]=V[QC]+Sr;
   {3.1} Swap P[Sr], P[QC];
   {3.2} P<<<1;

   The V’s update function is left unchanged. Permutation update function is improved by adding a default transformation. It can happened Sr and Qc to have the same value which will result in no change to occur in P, the circular-shift ensure that will not be the case.

   {4.1} Index=P[Sr]+P[QC];
   {4.2} Out=P[Index]+V[Index];

   The output is produced in slightly different way dominated by the state of P instead of linear combination as in EC-10.

   {5} Sr=P[Sr<<<1]+Out;

   NLS transformation is left unchanged.

4. Statistical Tests

SQ1-R passes the standard statistical tests of randomness; DIEHARD was used and 8-bit word version of SQ1-R. In order to further evaluate the statistical properties is should be confirmed:

1. 1.  
   2. Each element of P and V is equally used and changed
   3.  
   4. Sr, QC acts as independent entities.
   5.  
   6. The whole construction is Quasi-Entropy-Neutral-Transformation

In order to test the first property it is enough to count how many times each element of P and V is accessed and changed. {1} , {4.1} and {5} only access P or V without change. V is accessed twice per iteration, P is accessed four times, each iteration change two entries both in P and V. P is more accessed because SQ1-R is permutation cored. Since all the references to V and P are indexed with Sr and QC, it is enough to confirm that these variables during the generation have uniformly distributed values. The test strategy is quite simple, two separate output stream are isolated, one formed by the values of Sr and other by those of QS. If those sequences pass DIEHARD test than SQ1-R have all the properties stated above. Each iteration cause P to be left-circularly-shifted because of that calculating access and change rate of each entry should be done respecting this default transformation. In practice this left-circular-shift is never done directly but using a counter each reference to P is shifted right for the same value P should be left-circularly-shifted in that iteration. If the values of Sr are x₀, x₁, x_{2, …} then the entries of P effected in the i-th round are x₀, (x₁+1), (x₂+2) … [mod W] I is experimentally confirmed that Sr take uniformly distributed values even more the sequence produced from Sr values per round is pseudo-random. If non-random sequence is add to a random one the result is also random, because of this confirmation that Sr and QC based sequences are random is guarantee that all the entries of P are equally accessed and changed. Sr and QC sequences passed DIEHARD test.

It is interesting to test which is minimum length of P/V that will result in random sequences. All the results presented before are obtained using w=8 (P[0..255], V[0..255]). SQ1-R using 4-bit word is also secure. Since the output values are 4-bit long two subsequent values are combined into a byte.

The speed is a serious issue, Sq1-r is test in a pure DOS environment discarding the disk writes, Celeron 300 is used in tests. A single sequence 1GB long is generated. Aslo EC-8, EC-9, EC-10 are tested. Even surprisingly all of them show approximately the same speed 1.23 MB/s.

Appendix 2

Source Codes

/* EC-8 Stream Cipher file EC8.alg */

unsigned int P[256], Out, Counter, Sr;

int cc(void);

int gen(void);

int initialize(char*, int);

int gen(void) { return cc(); }

int initialize(char *key, int keylen) { return 0; }

int cc(void)

{

unsigned int t,a,b;

Counter++; Counter%=256;

a=P[Sr]; b=P[Counter];

t=P[a]; P[a]=P[b]; P[b]=t;

Out=P[(P[Sr]+P[Counter])%256];

Sr=((Out<<1)^(Out>>7))%256;

Sr=(P[Sr]+Out)%256;

return Out;

}

/* EC-9 Stream Cipher file: EC9.alg */

unsigned int V[256], Out, Counter, Sr;

int cc(void);

int gen(void);

int initialize(char*, int);

int gen(void) { return cc(); }

int initialize(char *key, int keylen) { return 0; }

int cc(void)

{

Counter++; Counter%=256;

V[Sr]=(V[Sr]+Counter)%256;

V[Counter]=(V[Counter]+Sr)%256;

Out=(V[Sr]+V[Counter])%256;

Sr=(((Sr<<1)^(Sr>>7))+Out)%256;

return Out;

}

/* EC-10 Stream Cipher file: EC10.alg */

#define WL 256

unsigned int P[WL], V[WL], Out, Counter, Sr;

int cc(void);

int gen(void);

int initialize(char*, int);

int gen(void) { return cc(); }

int initialize(char *key, int keylen) { return 0; }

int cc(void)

{

unsigned int T,a,b;

Counter++; Counter%=WL;

V[Sr]=(V[Sr]+Counter)%WL;

V[Counter]=(V[Counter]+Sr)%WL;

a=P[Sr]; b=P[Counter];

T=P[a]; P[a]=P[b]; P[b]=T;

Out=(V[Sr]+V[Counter]+P[(P[Counter]+P[Sr])%WL])%WL;

Sr=(P[((Sr<<1)^(Sr>>7))%WL]+Out)%WL;

return Out;

}

/* SQ1-R Stream Cipher file: SQ1-R.alg*/

#define WL 256

#define p(a) P[(a+R)%WL]

#define v(a) V[(a)%WL]

unsigned int P[WL], V[WL], Sr, R;

int init_sq(char*,int);

int sq(void);

int gen(void);

int initialize(char*, int);

int gen(void) { return sq(); }

int initialize(char *key, int keylen)

{

return init_sq(key,keylen);

}

int init_sq(char *keystream, int keylen)

{

int i,x;

x=0;

for(i=0;i<WL;i++)

{

P[i]=i;

V[i]=keystream[x]%WL;

x=(x+1)%keylen;

}

Sr=keylen;

for(i=0;i<WL;i++) for(x=0;x<WL;x++) sq();

return 0;

}

int sq(void)

{

unsigned int QC,T,Out,Index;

QC=p(v(Sr));

v(Sr)=(v(Sr)+QC)%WL;

v(QC)=(v(QC)+Sr)%WL;

T=p(Sr); p(Sr)=p(QC); p(QC)=T;

R=(R+1)%WL;

Index=(p(Sr)+p(QC))%WL;

Out=(p(Index)+v(Index))%WL;

Sr=((Sr<<1)^(Sr>>7))%WL;

Sr=(p(Sr)+Out)%WL;

return Out;

}

/* Stream Cipher Encryption Shell file: ss.c */

#include <stdio.h>

#include <string.h>

#include <stdlib.h>

#include <sys\timeb.h>

#include "" /* .alg file for example "sq1-r.alg" */

int main (int argc, char **argv)

{

FILE *outf;

int c;

unsigned long i,j,k,size;

unsigned long PP,TT,GG;

struct timeb st,en;

ftime(&st);

GG=0;

if(argc==1)

{

printf("SS [output file] [size] [key] \n");

return 0;

}

outf=fopen(argv[1],"wb");

size=atoi(argv[2]);

initialize(argv[3],strlen(argv[3]));

TT=(long)size*1024L*1024L; TT/=100;

for(i=0;i<size;i++) for(k=0;k<1024;k++)

{

for(j=0;j<1024;j++)

{

c=gen();

putc(c,outf);

}

PP=i; PP*=1024L; PP+=k; PP*=1024L; PP+=j;

PP/=TT;

if(PP>GG) printf("\r Generated: %ld%% ",PP);

GG=PP;

}

printf("\n");

fcloseall();

ftime(&en);

TT=en.time-st.time; TT*=1000; TT+=(en.millitm-st.millitm);

printf(" Total time: %ld.%ld s\n",TT/1000, TT%1000);

return 0;

}