Kostadin
Bajalcaliev
Institute
of Informatics – Skopje
kbajalc@eon.pmf.ukim.edu.mk
http://eon.pmf.ukim.edu.mk/~kbajalc
May
7, 2001
From
the beginning of the electronic era in cryptography the main
block-cipher design model had stayed the same, the concept of
mixing substitution and transposition. Differential cryptanalysis
and Liner cryptanalysis are applicable on the majority of the
Feistel-Network based ciphers, and they have, at least in theory,
shown the weakness of this model. There is a growing disparity
between the ability to design secure ciphers and the
cryptanalysis. This indicates that block cipher design converge
to “maximum secure cipher”. Polymorphic Encryption and the
Quasi Function theory are a concept how to design a cipher having
the properties of a Maximum Secure Cipher. The new design
paradigm is KEY=ENCRYPTION ALGORITHM, ciphers designed in a way
that each key present a different encryption algorithm.
keywords:
cryptography, block-cipher, stream-cipher, security, polymorphic
encryption, quasi function
The best representative of the classical block-cipher design paradigm is Feistel Network with its most prominent realization, the Data Encryption Standard. The security in this approach is determined by the non-linearity of the S-box. Even there have been a wide interest and discussion about the design of S-boxes there is no algorithm proposed for generating “secure S-box”. Maybe the invention of Differential and Linear cryptanalysis is the final word about this paradigm. DES-like ciphers are not candidates for Maximum Secure Cipher.
Maximum
Secure Cipher (MSC) is an encryption algorithm immune
to all possible (existing and to-be-invent) attacks. Existence of
an attack against MSC implies a need for a significant knowledge
about the key as a precondition to launch it. The growing
disparity between the advance of the cipher-design and the
cryptanalysis indicate a convergence in the process of developing
secure ciphers. The limit of this process is the MSC.
The MSC should be immune to any kind of attack that is trying to discover the key without a prior knowledge about it. The classical approach promote the use of fixed transformation, the key and plaintext enter a predefined sequence of transformations. Both the key and the plaintext have no impact on the algorithm, c=E(k,p) concept. Because of this the properties of f can be independently analyzed abstracting the key and the plaintext. As the history has shown there is an alternative approach. RC5 has introduced the data-depend-rotation. This is the simplest instance of what is going to be described here as Polymorphic Encryption. Instead of being a passive object of transformation, the plaintext determines part of them. The history of science is showing that each improvement in the human ability to understand the nature or to construct something lead to a discovery of at least one new problem. Because of this, it is an imperative to acknowledge the boundaries of advance concerning a given problem. Having cryptography in mind, the problem of designing secure cipher is equivalent to the problem of estimating the efficiency of the possible attacks. This implies existence of two distinct classes of solutions. The first approach is to design cipher immune to the attack, and the second to design cipher incompatible to the attack. For example, there is no use of Differential cryptanalysis if the cipher is not Feistel-Network based. MSC should be designed to be incompatible to any kind of attack assuming the secrecy of the key.
The Polymorphic Encryption is a general concept applicable in MSC design. The idea is originally presented in 1997 in ANIGMA [1] cipher and MEX [2] hash algorithm. Consequently, there are several different implementations: A2 [3], SQ2 [4], Z876 [5]. These algorithms present the evolution of the theory presented in this thesis as well as the previously published draft version of this thesis [6]. The goal is to construct a cipher that act significantly different according to the key. This is an analogy of the nature, the key is the DNA and the cipher is the body. The encryption algorithm specifies a template what should happen, but DNA - the key, determines how it is going to, the cipher is an algorithm that generate an encryption function according to the key.
The essentials in the human activities are the algorithms, exact methods how to do something. Behind each algorithms there is a problem, the algorithm is a way to solve the problem. The problem is the meaning of the algorithm, for example P=a2 is recipe how to calculate the area of a square. Clearly, there is a connection between the area and the length of the square side, the algorithm is a realization of this connection. Let y=P(x)= x3-7x2+x-5 is a relation between the property x and y of a given object expressible as numerals. In prefix notation P(x) is: P(x)=+(-(^(x,3),*(7,^(x,2)),-(x,5)). Each operation +,-,*,^ as defined in the arithmetic is a function taking two arguments. Let each operation is substituted with o - general operation (in this case any binary operation).
![]()
The first expression contain the all the information as P(x) except the operations to be executed over each pair of operands enclosed in parenthesis, this is First Degree Quasi Function corresponding to P. The second expression only respects the original order of operations and the operands but does not the hierarchy, this is Second Degree Quasi Function corresponding to P. P’ and P’’ define classes of functions, inserting different combinations of operations between (or before, depends on notation) the operand pairs result in different functions, but all of them having the same template. Because of simplicity expressions like P’’ are defined to be equivalent to ((….(a,b),c),d)….),z).
First
Degree Quasi Function corresponding to P, denoted as
Qf(P) or P’ is the set of all functions having the same
operands, the same operand order and hierarchy. The operations
are abstracted.
Second
Degree Quasi Function corresponding to P, denoted as
Qf2(P) or P’’ is the set of all
functions having the same operands and operand order. The
hierarchy and the operations are abstracted.
Two
functions F and G are Quasi Equivalent if
Qf(F)=Qf(G).
Quasi
Algebra of degree k, denoted QAk
is a set of functions {f,g,h…} with a fixed number of arguments
k. Each function of QAk have the form
y=w(x1,x2…,xk).
Degree of
a Function is the number of operations in the
function, denoted |F|.
All this is applicable only on algebraic expression, there is no Qf(sin(x)). Because of this Quasi Algebra is defined as a base to construct quasi functions. By having fixed number of arguments, assuming each function have k-arity then each operation place in the Qf(P) can be filled with any of the available operations. The simplest or polynomial algebra is {+,-.*,/,^}. Working in the digital world has some advantages, the basic algebra can be extended with logical bit-wise operations like xor.
If P is written in assembler stile than it will be:
R=0
T=x^3
R=R+T
T=x^2
T=-7*T
R=R+T
T=x-5
R=R+T
This can easy be translated to run on any processor. The essential information needed to calculate anything is {operands, operation, where to store the result}, generalizing operation into a class of similar operations result in QF(ALG) the Quasi algorithm corresponding to ALG.
Taking the previous example F = o(o(o(x,3),o(7,o(x,2)),o(x,5)) ; then s(a) = (+,-,^,*,^,-), where s denote a variation of the quasi algebra a (a by definition is a set of operations). In order to simplify the expression the F notation is defined as: F(F,s(a),y) denote a function having First Degree Quasi Function F, operations specified with the vector s(a) and argument(s) y.
F(o(o(o(x,3),o(7,o(x,2)),o(x,5)),(+,-,^,*,^,-),x)=
x3-7x2+x-5
This is a practical way to express quasi functions. Using this notation F(F,S(a,|F|),y) where S(a,|F|) is a set of all possible variations a of order |F| (the degree of function F) denote all the functions having template F and argument(s) y.
Any function defined over a Quasi Algebra has its Quasi Function. Crucial for quasi functions is to define the algebra they are going to use. Not only arithmetic operations can be used to form the QA, any function can be included, for example W=(f(x,y),g(x,y),h(x,y)) where f,g,h are some two argument functions is also a quasi algebra. The Quasi Algebra is always a finite set of functions and the functions defined in the algebra are defined over a common set. In this thesis all the functions are defined over a discrete set [0...2n] using mod 2n arithmetic. Not only binary functions, but any k-arity function can be used to define the QA set. For example
f(x,y,z)=x*y-z,
g(x,y,z)=(z+y)*z, h(x,y,z)=x+y+z,
Q=(f,g,h)
R=((a,b,(c,a,d)),((a,c,c),b,(c,a,b)),c)
F(R,S(Q,|R|),(a,b,c))
Q is a regular quasi algebra, R is a regular quasi function in respect to Q, and F is the set of all possible function f(a,b,c) defined over Q such as f’=R.
Having this in mind F(F,s(a),y) can be viewed as Quasi Function Processor. Its role is to calculate the value of (F, s(a)) for the values of the function arguments given with y. Quasi Functions are reality and can be widely used, especially in cryptography. The main characteristic is the inability of mathematics to analyze this kind of functions. The whole science we have today is base on the function-concept y=f(x), but there is nothing compatible with Quasi Functions. Here is a simple example,
f(x)=(1+1/n)n;
lim f(n) = e, n ® µ
F(n)=f’(n)=o(o(1,o(1,n)),n)
a=(+, /, ^)
f(n)= F(F,(^, +, /),n)
lim F(F,s(a),n)
= ? n ® µ
There is not way to calculate lim F(F,s(a),n) n ® µ except to try all possible variation s(a). Since there only 3 operation places and only 3 operation included in the algebra it will be easy. The result is going to be a set of limits, not a single value. However there is not method to determine this set without a brute-force. The variation s(a) can also be expressed like a function of a controlling input D, s=W(D,a); F(F, W(D,a),y). The practical usage of this property is explained letter. If the controlling signal D is expressed in terms of y the resulting function F(F, W*(y,a),y) is a one-way function. Introduction of the theory of Quasi Functions is most probably a solution to the enigma of existence of one-way functions.
Polymorphic Encryption is a realization of the Quasi Function theory. Cryptography can benefit form QF theory more than any other science. As stated in the beginning of this thesis the goal is to construct Maximum Secure Cipher. Instead designing ciphers immune to cryptanalytic attacks the opposite approach is choused, designing ciphers to be incompatible to the attacks possible at the present level of science. Quasi Functions are incompatible to all the methods of analysis known today, mathematics is unable to analyze QF. Cryptanalysis is based on assumption that each pair (p,E(p,k)) leak some information about the key, the ciphers are braked by finding a way to collect this information. This approach presumes the encryption algorithm and the key to be independent one from another. The situation drastically changes if the Encryption algorithm is equivalent to the key. Here is a hypothetical cipher:
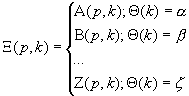
A,B…Z are distinct encryption algorithms, a,b…z are distinct number and Q is a condition function. The ideal case will be |K|=|Img(Q)| each key to specify a different algorithm. X is a Quasi Function X=F((k,p),W(a,k),(k,p)) where a is {A(p,k), B(p,k)… Z(p,k)}. This concept is exactly what has been defined as Maximum Secure Cipher. Using the QF notation Polymorphic Encryption Algorithm is defined as:
F – Quasi
Function
a - Quasi
Algebra
W -
Variation generator (over the set a, having degree |F|, according
to the value of k1)
y = (p,k2)
c = F(F, W(k1,a),(p,k2))
Existence of F-1 in general case is uncertain. Even more, it is hard to construct reversible quasi functions. If the cipher is constructed like X in the previous example and assuming A-1,B-1…Z-1 exist then X-1 exist also. But using the Feistel Network any function can be utilized in building block ciphers.
Any polynomial function have a template F(x)=o[…o[o[m(an,p(x,n)),m(an-1,p(x,n-1))],m(an-2,p(x,n-2)]…m(a0,p(x,0))]. Substituting all “o” with “+”, “m” with “*”, “p” with “^” F(x) will result in polynomial expression. Excluding the constants from the expression result in Quasi Polynomial. Those quasi polynomials are easy to be implemented in software what makes them a good choice when designing a polymorph cipher. The general form of quasi polynomials is:
![]()
Using a quasi polynomial QP(x)=o1(o2(o3(o4(a1,x),o5(a2,x)),o6(a3,x)),o7(a4,x)) a simple encryption algorithm can be realized. k1 is a vector of operations (o1, o2, o3, o4, o5, o6, o7) and k2 is a vector of coefficients (a1,a2,a3,a4). The key space is a set of all possible pairs (k1,k2).

Incorporating R(x,k) function into a Feistel Network is enough to construct a block cipher. This cipher is characterized by its unpredictability since each key defines different quasi polynomial that is used as a Round function. Polymorphic Encryption Cipher (PEC) is acting as F - processor. The key is determining the transformations to be done and the template F determines the structure. There are three classes of quasi functions as defined below:
Type-1.1: F(
F, k1, (y, k)))
k1 is an operation vector (a variation of the Q Algebra a with degree |F|) which is independent from k2 the predefined coefficient vector.
Type-1.2: F(
F, W(k,a), (y,G(k)) )
Instead of having two separate keys - vectors, it is easier to construct function W and G that produces the operation and the coefficient vector from the key.
Type-2: F( F,
W(y,a), (y,G(k)) )
The operation vector is produced according to the value of y. The value passed to the argument of Fs where s = W(y,a) is also used to calculate s. This is a prototype of one-way function.
Type-3: F( F,
W((k,y),a), (y,G(k,y)) )
Both k and y are used to compute the variation s, and both of them to compute the coefficient vector.
Type-1 is appropriate for block cipher design because independence of y and k assure a better distribution of the output.
If a
function f(x), f:D®D is not 1-1 mapping over a discrete set D
then |Img(f)|/|D| is defined to be distribution
coefficient denoted DC(f).
Ideal case is to have DC(f)=1. Because Quasi Functions in general are not 1-1 mapping the distribution coefficient is less than 1, functions having greater DC are better.
As noted before ANIGMA [1] is the first
representative of Polymorphic Encryption Ciphers. It is a very
simple design, the key is expanded to fill E_Table[16][4] array
of 32 bit words and R_Table[14][4] a 2 bit word array. There four
functions used F[0], F[1], F[2] and F[3] respectively defined as
(usign the C-like notation).
F[0](x,y,z) = x
& y | ~x & z
F[1](x,y,z) = x
& z | ~z & y
F[2](x,y,z) = x
^ y ^ z
F[3](x,y,z) = y
^ (x | ~z)
The cipher is consisted of 16 round and each of them consists of:
for round=0 to
number_of_rounds
{
block[0]+=E_Table[round][0];
block[1]+=E_Table[round][1];
block[2]+=E_Table[round][2];
block[3]+=E_Table[round][3];
block[0] +=
F[R_Table[round][0]](block[1],block[2],block[3]);
block[1] +=
F[R_Table[round][1]](block[0],block[2],block[3]);
block[2] +=
F[R_Table[round][2]](block[0],block[1],block[3]);
block[3] +=
F[R_Table[round][3]](block[0],block[1],block[2]);
}
ANIGMA use Type-1 quasi function R=(x,y,z) and algebra {F0,F1,F2,F3}. There is only one operation place in R, and no coefficients.
SQ2 [4] is the next step in the evolution of Polymorphic Encryption. The quasi function used in this cipher is Type-3. It is an interesting design solution, R=(…((x,S’),S’’)…),S(n)), S is array of 16 32-bit numbers generated according to the key. The function has a recursive definition.
for(i=0;i<Length_of_function;i++)
{
r=(x*(x+11));
switch((int)(r>>30))
{
case 0:
x+=S[(int)((r>>26)%16)]; break;
case 1:
x*=S[(int)((r>>26)%16)]; break;
case 2:
x^=S[(int)((r>>26)%16)]; break;
case 3:
x-=S[(int)((r>>26)%16)]; break;
}
}
This is a very elegant solution but the distribution coefficient of this kind of function is expected to be very low. Because of this the next cipher in line is going to use Type-1 functions again. Z876 [6] is design to be used in environments where key-setup is unwelcome solution.
P[3]+=P[0]+P[1]+P[2];
if(P[3]{30}==1)
P[0]+=F[P[3]{30,31}](P[1],P[2]);
else
P[0]^=F[P[3]{30,31}](P[1],P[2]);
P[1]>>>P[0]{28,31};
P[2]>>>P[0]{24,27};
P[3]>>>P[0]{20,23};
P<<<1;
S{m,n} denote the value of the bit sub-string formed by the m-th to the n-th bits of S. Z876 use a simple quasi function F=(x,y) defined as R[d](x,y) ={(x+y; if d=0), (x-y, if d=1), (x xor y; if d=2), (x*y; is d=3)}. The algebra is {+,-,*,xor}, this is de facto standard algebra in the computer cryptography. Z876 have two stage round function. The first stage is UFN 67:32, P[0] is the target, P[1], P[2] are the source and three bits of P[3] are used to chouse the operations in the round. The second stage is consisted of rotations according to the 25 LSB of P[0], this is UFN 25:96. Being an incomplete UFN is a big disadvantage of Z876.
Polymorphic Encryption is a strong strategy against any kind of attack. There is certain equivalence between the key and the encryption algorithm. Polymorphic ciphers are not functions in the real sense of the term. All the ciphers designed using Polymorphic Encryption theory can be viewed as templates specifying the process down to elementary transformations. The key is upgrading this template to an encryption algorithm by specifying the elementary transformations to take place. This design strategy is going to be explained within the analysis of SQ5.
It is hard to design reversible functions, but the Feistel networks aloud any function to be turned into 1-1 mapping. Because of this FN are popular method in block cipher design, but the classical usage of FN utilizing a predefined S-box has shown to be insecure. SQ5 Feistel network is design respecting the results and recommendations presented in “Unbalanced Faistel Networks and Block-Cipher Design” [7]. SQ5 is a 128 bit cipher build upon a UFN 96:32. The round function is very simple.
B0=B0
xor F( F, W(B3,a), (B1,B2,G(B3,KEY))
)
B<<<1
The build block in SQ5 is a polymorphic function defined over the standard algebra {+, -, *, xor}. In each round, the first sub-block B0 is changed according to the value of the others. The last sub-block B3 is used as a controlling signal for W - function generating the operation vector and G - function generating the coefficient vector. The key is passed as an argument to G controlling the coefficients generation. In practice G and W should be a simple or pre-computed functions. The quasi function used is F=o3(o2(o1(o0(c0,A),c1),B),c2) where A and B are arguments, (c0,c1,c2) is the coefficient vector and (o0,o1,o2,o3) is the operation vector.
Using a polymorphic function result in SQ5 being a hyper-heterogeneous FN. As stated in [5] ciphers having heterogeneous FN i.e. F function which treating different sub-blocks differently are more likely to be immune to differential cryptanalysis.
Hyper-heterogeneous
is the Feistel Network that is designed to have multiple
F-functions and the schedule of their use is key/data-depended.
MSC should be hyper-heterogeneous FN.
Using more human readable form SQ5 quasi function is defined as follow.
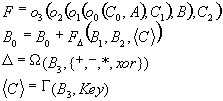
The operation vector is generated according to B3, which is a data-depend transformation, the same happens with the coefficient vector. Even this is so the quasi function used in SQ5 is Type-1. Using this data-depended transformation result in fast difference propagation. SQ5 have 16 rounds, and a cycle of length 4. In each cycle, every bit is once a part of the controlling word, one a part of the target block and twice a part of the source block. It is very important to construct complete UFN, i.e. all block bits in a round to be active, as a part of the target or the source. G and W must be constructed to utilize all the bits of D=B3 the controlling signal. Since SQ5 polymorph function is Type-1 there should be no overlap in the bits used by G and W. The polymorph function F has also been design to support the balanced and complete usage of the Controlling signal bits.
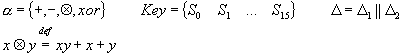
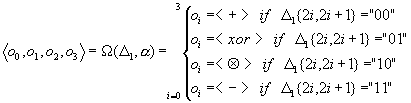
G and W utilize all the bits of the controlling signal D. The 8 most significant bits D1 are used to generate the operation vector, this is a simple mapping 22®a. The rest of 24 bits D2 is used to generate the coefficient vector. The key is presented to the algorithms as an array of 16 32-bit numbers. The coefficient generation process is design by the following rationale; 3 coefficients are needed and there is 24 bits left, so each coefficient should utilize an 8 bits in order to completely use the controlling signal. Four of those 8 bits are used to chouse one of the 16 32-bit values and the other 4 to cycle shift it. The resulting cipher is complete UFN.
All the operations are done ever a GF(232), except for the multiplication GF(232) is a group regarding the addition, subtraction and xor. Instead of the regular multiplication SQ5 use a (x A y)=x+xy+y. This is needed in order to avoid the zero problem (0 * x)=0, but 0 A x = x. SQ5 security is based on the assumption that analyzing quasi functions will be infeasible for considerably long period. It can not be claimed there will be no attack against quasi functions but its existence will certainly be a result of a revolution in the present postulates of science. It is infeasible to analyze Quasi Function base ciphers, all present attacks are aimed at homogeneous FN or heterogeneous FN with a fixed schedule of functions. Any polymorph encryption algorithm by definition has more then a single F-function and a data-depend strategy for their scheduling. There are 256 different operation vectors, and 512 bits of key material presented to the algorithm as array of 16 32-bit words. Having 512 bits of key material is impractical, so a key expansion algorithm can be used to expand a conventional 128-key into the needed 512 bits. The specification of SQ5 [8] defines all the aspects of the cipher.
Quasi Functions can be used in Stream Cipher design as well. The classical approach of stream cipher design is explained in “Stream Cipher Design Postulates – SQ model” [6]. However it turns out that not only the classical techniques are promising when the SC design is in question. SQ6 is a stream cipher using the same design postulates as SQ5, they are very similar in structure W, G, F, a and Key are analogously defined. Since SQ6 is a stream cipher a counter p is included in the design. W is redesigned to step the counter. Incorporating the counter, F and W are slightly changed.
![]()
p is the dynamic counter, in each iteration the counter is steeped 4 times by distinct values corresponding to different values of the 8 bits of the controlling signal passed to W. Since the counter is used to chouse which entry of the RPool is going to be changed in the current iteration its values are limited in the interval [0,15]. The stepping constants are chosen to be half odd, half even. Also there is a additional property 5+8=13, 8+11=3, 11+12=7, 5+11=0, 5+12=1 mod 16, all the prime numbers less then 16 can be expressed as addition of {5,8,11,12}. This is important for a counter to have uniform distribution. Instead of the data-block present in SQ5, SQ6 use four registers R0, R1, R2, R3 in a equivalent way as SQ5. Instead of key there is a Randomness Pool substituting what is Key in SQ5. Finally the iteration of SQ6 is defined as:
P=F(F, W(R3,p4k,a),
(R1,R2,G(R0,RPool)))
C=p4(k+1)
Wk=R0+SC
R0=R0+P
SC=SC+(P>>>C)
R<<<1
SQ6 has pass all the statistical tests of randomness. Instead of using a standard approach SQ6 use the properties of the quasi functions to produce randomness, it is secure since there is no way to predict the behavior of a quasi function. The output of the algorithm is formed as a addition of R0 and SC but immediately after they are used their values is changed using P the result returned by the Polymorph function. Detailed description of SQ6 is available in [9].
Quasi functions have been described here as well as introduction of notation and an initial analysis of their properties and the potential benefits for cryptography. Polymorphic Encryption is a strategy of designing cipher by utilizing the properties of Quasi functions. Not only the cryptography should benefit from the further research of the Quasi functions and their properties. As long as the present state of art in mathematics and cryptography is concerned Quasi Functions are totally incompatible concept and non-of the existing techniques of function analysis is applicable on Quasi Functions. Block and Stream ciphers designed using quasi functions have MSC level of security in respect to the present advance of science. From an implementation aspect the quasi functions are easy and compatible to the present hardware and software.
This thesis has reference prior works of the same author as well as works of other authors. This is a complete list of referenced materials:
[1] ANIGMA, Kostadin Bajalcaliev 1997
[2] MEX, Kostadin Bajalcaliev 1997
[3] A2, Kostadin Bajalcaliev 1998
[4] SQ2, Kostadin Bajalcaliev 1999
[5] Z876, Kostadin Bajalcaliev 2000
[6] “Quasi Algorithms / Quasi Functions; Polymorph Encryption” ver. 0.9 K. Bajalcaliev 2000
[7] “Unbalanced Feistel Network and Block-Cipher Desing”, Bruce Schneier and John Kelsey, availble at http://www.counterpane.com
[8] SQ5, Kostadin Bajalcaliev, 2001
[9] SQ6, Kostadin Bajalcaliev, 2001
[1-6] and [8-9] are all available at http://eon.pmf.ukim.edu.mk/~kbajalc